今回はPythonの数値計算ライブラリ、SymPyを使って積分を計算する方法を解説します。
SymPyとは
SymPyとはPythonで利用可能な代数計算ライブラリです。
因数分解、微積分、三角関数、行列計算など様々な数値計算をライブラリを使って簡単に実行することができます。
公式サイトは以下となります。
SymPyをインストールする
SymPyをインストールするため、以下のコマンドを実行してください。
pip3 install --upgrade pip
pip install sympy積分の公式
今回はSymPyを使って積分の計算を実行してみます。
手計算でも結果の確認をしますので、積分の公式を確認します。
不定積分の公式
不定積分の公式は以下となります。Cは積分定数です。
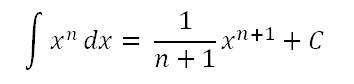
定積分の公式
定積分の公式は以下となります。
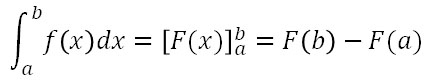
SymPyで積分を実装する
SymPyで積分の計算を実装する方法は以下の通りです。
計算で使用する変数をシンボルとして以下のように定義します。
x = Symbol('x')今回は以下の式を計算してみます。
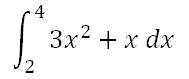
この式をPythonで以下のように記述します。Pythonではべき乗は「**」と記述します。(今回はxの2乗なのでx**2と書きます)
expr = '3*x**2+x'積分を実行するためintegrateメソッドを使用します。
引数で式と積分範囲を指定します。
ans = integrate(expr, (x, 2, 4))作成したソースコード
実際に積分の計算を行うコードは以下の通りです。
from sympy import integrate, Symbol
x = Symbol('x')
#積分の対象となる式
expr = '3*x**2+x'
#不定積分
ans1 = integrate(expr,x)
#定積分
ans2 = integrate(expr, (x, 2, 4))
#計算結果
print("不定積分の結果:", ans1)
print("定積分の結果:", ans2)実行結果
Pythonの計算結果と手計算の結果を比較してみましょう。
プログラムの実行結果
実行結果は以下の通りです。
不定積分の結果: x**3 + x**2/2
定積分の結果: 62不定積分の結果の式についてはPythonの表示が少しややこしいですが、「X**3+(X**2)/2」という意味になりますので注意が必要です。
手計算の結果
続いて同じ計算を先ほどの公式を使って手計算で解いてみます。
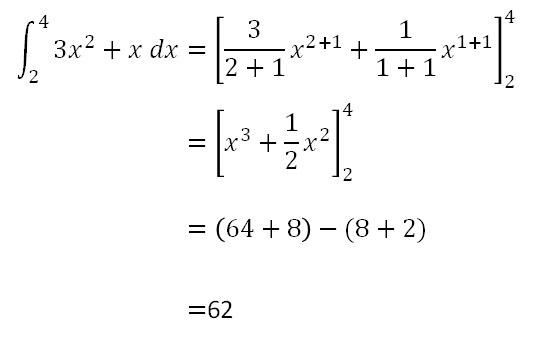
SymPyでの結果と一致しましたので正しいことが確認できました。
まとめ
今回はSymPyを使って積分の計算を実行する方法を解説してみました。SymPyを使うと数年前は非常に高額な数値計算ソフトを使わなければできなかったような計算が簡単に実装できますので、ぜひ積分以外の計算でも活用してみてください。
また、以下の記事で効率的にPythonのプログラミングスキルを学べるプログラミングスクールの選び方について解説しています。最近ではほとんどのスクールがオンラインで授業を受けられるようになり、仕事をしながらでも自宅で自分のペースで学習できるようになりました。
スキルアップや副業にぜひ活用してみてください。

スクールではなく、自分でPythonを習得したい方には、いつでもどこでも学べる動画学習プラットフォームのUdemyがおすすめです。
講座単位で購入できるため、スクールに比べ非常に安価(セール時1200円程度~)に学ぶことができます。私も受講しているおすすめの講座を以下の記事でまとめていますので、ぜひ参考にしてみてください。

それでは、また次の記事でお会いしましょう。













コメント